반응형
포인터를 통해 이진 탐색 트리를 간단히 만들어 보자.
이진 탐색 트리 개념
이진 탐색 트리(Binary Search Tree) 개념
이진 탐색 트리(Binary Search Tree)의 정의 1. 각 노드가 최대 두개의 자식을 갖는 탐색 트리이다. 2. 왼쪽 자식은 부모보다 키 값이 작고, 오른쪽 자식은 부모보다 키 값이 크다. Key값이 8, 3, 10, 1, 6, 14,
www.crocus.co.kr
배열을 이용한 이진 탐색 트리
배열을 이용한 이진 탐색 트리(Binary Search Tree) 소스 코드
insert(number X, node N) if X가 노드 N에 있는 숫자보다 작다면 if N의 왼쪽 자식이 없다면 X를 포함하는 새 노드를 만든 뒤, N의 왼쪽 자식으로 만든다. else insert(X, N의 왼쪽 자식) else X가 노드 N에 있는..
www.crocus.co.kr
lagacy 코드
이진 탐색 트리(Binary Search Tree) 소스 코드
이전 게시물에서 이진 탐색 트리의 개념을 설명하였다. 코드로 옮기기 전, insert에 대한 코드는 아래와 같이 작성하면 된다. insert(number X, node N) if X가 노드 N에 있는 숫자보다 작다면 if N의 왼쪽 �
www.crocus.co.kr
#include <iostream>
#define MAXROW 5
typedef struct NODE
{
int key;
int value;
struct NODE *left;
struct NODE *right;
}NODE;
NODE *root;
// 초기화
int init(int key, int val)
{
// 가장 처음에 들어오는 값은 루트가 된다.
NODE *newNode = (NODE*)malloc(sizeof(NODE));
newNode->key = key;
newNode->value = val;
newNode->left = NULL;
newNode->right = NULL;
root = newNode;
return 1;
}
// 삽입
int insert(int key, int val, NODE *pt)
{
NODE *temp = pt;
// val가 현재 보고있는 노드의 값 보다 작다면
if (val < temp->value)
{
// 왼쪽이 비어있으면
if (temp->left == NULL)
{
// 해당 부분에 삽입
NODE *newNode = (NODE*)malloc(sizeof(NODE));
temp->left = newNode;
newNode->key = key;
newNode->value = val;
newNode->left = NULL;
newNode->right = NULL;
}
// 비어있지 않다면 왼쪽으로 이동
else
{
insert(key, val, temp->left);
}
}
// val이 노드에 값보다 보다 크거나 같다면
else if (val >= temp->value)
{
// 오른쪽이 비어있으면
if (temp->right == NULL)
{
// 해당 부분에 삽입
NODE *newNode = (NODE*)malloc(sizeof(NODE));
temp->right = newNode;
newNode->key = key;
newNode->value = val;
newNode->left = NULL;
newNode->right = NULL;
}
// 비어있지 않다면 오른쪽으로 이동
else
{
insert(key, val, temp->right);
}
}
return 1;
}
// 이진 탐색 트리 출력(전위 순회)
void binaryTreePrint_preOrder(NODE *node) {
if (node == NULL) {
return;
}
int key = node->key;
printf("key : %d value : %d\n", node->key, node->value);
binaryTreePrint_preOrder(node->left);
binaryTreePrint_preOrder(node->right);
}
int main()
{
int bst[MAXROW][2] = {
{3, 17},
{1, 18},
{5, 20},
{4, 20},
{2, 15}
};
// 이진 트리 데이터 삽입
for (int i = 0; i < MAXROW; i++)
{
if (i == 0)
init(bst[i][0], bst[i][1]);
else
insert(bst[i][0], bst[i][1], root);
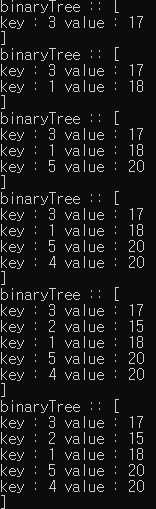
printf("binaryTree :: [ \n");
binaryTreePrint_preOrder(root);
printf("]\n");
}
// 이진 트리 데이터 출력
printf("binaryTree :: [ \n");
binaryTreePrint_preOrder(root);
printf("]\n");
return 0;
}
반응형
'Applied > 자료구조' 카테고리의 다른 글
| Parent, Child, Sibling 구조의 Tree (0) | 2019.09.10 |
|---|---|
| 해싱 기법 소스 코드(No STL) (0) | 2019.04.01 |
| 정적 할당을 이용한 Trie (2) | 2019.03.29 |
| 재귀가 아닌 반복문을 이용한 Trie (0) | 2018.03.07 |
| 힙(Heap) 자료구조 (4) | 2018.03.04 |