기계학습 문제
기계학습 문제는 분류(Classification)와 회귀(Regression)로 나눌 수 있다.
이때 분류는 데이터가 어느 클래스에 속하느냐의 문제이고, 회귀는 입력 데이터에서 연속적인 수치를 예측하는 문제이다.
이렇듯, 신경망의 출력층에서는 항등 함수와 소프트맥스 함수를 이용하여 출력 값을 얻을 수 있다. 이는 분류와 회귀에 있어서 중요한 역할을 수행하게 된다.
기계학습의 문제풀이
또한, 기계학습의 문제풀이는 학습과 추론(Inference)의 두 단계를 거쳐 이뤄진다.
학습단계에서 모델을 학습하고, 추론 단계에서 앞서 학습 된 모델로 미지의 데이터에 대해서 추론(분류)을 수행한다.
추론단계에서는 출력층의 소프트맥스 함수를 생략하는 것이 일반적이다.
추론과정을 신경망의 순전파(Forward Propagation) 이라고도 한다.
한편, 신경망을 학습시킬 때는 출력층에서 소프트맥스 함수를 사용한다.
1. 항등 함수(Identity Function)
항등 함수는 입력을 그대로 출력한다. 즉, 입력과 출력이 항상 같다는 의미이다.
따라서 출력층에서 항등 함수를 사용하면 입력 신호가 그대로 출력 신호가 된다.
항등 함수의 처리는 신경망 그림으로는 아래와 같다.
이때 항등 함수에 의한 변환은 은닉층에서의 활성화 함수와 마찬가지로 화살표로 그릴 수 있다.
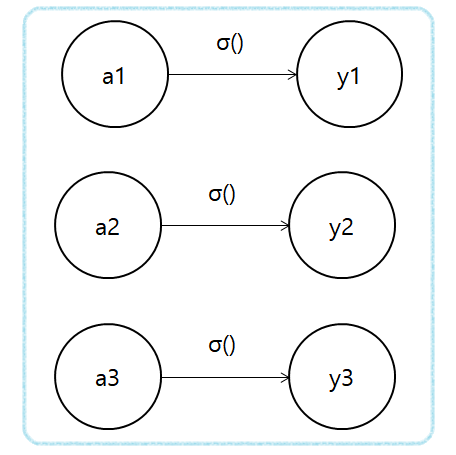
2. 소프트맥스 함수(Softmax Function)
소프트맥스 함수는 분류에서 사용하고 식은 다음과 같다.

exp(x)는 지수함수(Exponential Function)이다(e는 자연상수).
n은 출력층의 뉴런 수, yk는 그 중 k번째 출력을 뜻한다.
위 식과 같이 소프트 맥스 함수의 분자는 입력신호 ak의 지수함수, 분모는 모든 입력 신호의 지수함수의 합으로 구성된다.
이 소프트맥수 함수를 그림으로 나타내면 다음과 같다. 그림과 같이 소프트맥스의 출력은 모든 입력 신호로부터 화살표를 받는다.
출력층의 각 뉴런이 모든 입력 신호에서 영향을 받기 때문이다.

이제 이를 코드로 나타내면 다음과 같다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | import tensorflow as tf import numpy as np def softmax(a): expA = np.exp(a) # 각각의 지수 함수 print(expA) sumExpA = np.sum(expA) # 시그마 부분의 지수 함수 print(sumExpA) y = expA / sumExpA print(y) a = np.array([0.5,3.1,2.0]) softmax(a) [ 1.64872127 22.19795128 7.3890561 ] 31.235728651072414 [0.05278319 0.71065899 0.23655783] | cs |
이때 소프트맥스 함수를 위와 같이 구현하는게 맞는 것이지만
a = np.array([1000.0,2000.0,3412.0]) 만 들어와도 오버플로우가 발생한다
따라서 소프트맥스 함수 구현을 아래와 같이 수정 할 수 있다.

바로 구현을 해보자.
컴퓨터에서 오버플로우 없이 이용 할 수 있는 소프트맥스 함수
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | import tensorflow as tf import numpy as np def softmax(a): c = np.max(a) print(c) expA = np.exp(a - c) # 각각의 지수 함수 print(expA) sumExpA = np.sum(expA) # 시그마 부분의 지수 함수 print(sumExpA) y = expA / sumExpA print(y) a = np.array([0.5,3.1,2.0]) softmax(a) 3.1 [ 1.64872127 22.19795128 7.3890561 ] 31.235728651072414 [0.05278319 0.71065899 0.23655783] | cs |
이때 이렇게 c라는 상수를 써도 되는 이유는 소프트맥스 함수의 출력은 0에서 1.0 사이의 실수이기 때문이다.
또한 소프트맥스 함수의 출력의 총합은 1이다.
출력 총합이 1이된다는 점은 소프트맥스 함수의 중요한 성질이다.
이러한 성질 때문에 함수의 출력을 "확률"로 해석하여 "분류(Classification)"를 할 수 있는 것이다.
위의 값을 보면 y[0]는 0.052(5.2%) y[1]은 0.710(71.0%) y[2]는 0.236(23.6%)이며 이를 다 합하면 100%가 됨을 알 수 있다.(지금은 소수 둘째자리부터 버려서 99.8%인데 다더하면 100%이다.)
따라서 이러한 소프트맥스 함수를 이용하여 확률로 나타내고 이 입력에 대해서는 y[1]이 71%의 확률로 답에 가장 가깝다라고 할 수 있다는 것을 알 수 있다.
출처 :밑바닥부터 시작하는 딥러닝
'Applied > Artificial Intelligence' 카테고리의 다른 글
| numpy를 이용한 행렬 계산 (0) | 2019.06.06 |
|---|---|
| 심층 신경망 구현 예제 (0) | 2019.06.05 |
| 활성화 함수(Activation Function) (0) | 2019.06.03 |
| 퍼셉트론 (Perception) 알고리즘 (0) | 2019.06.02 |